The rule of 72

As many of us know, investing our hard-earned cash can be an effective way to allow us to live the lives we want.
If structured appropriately, the fascinating results of “compounding” can provide a powerful boost to investment returns. Even Einstein is alleged to have claimed it as the “eighth wonder of the world” and “the most powerful force in the universe”.
But a question many investors like to ask is, “how long could it take for my investment to double?”
Whilst we always explain to our clients that this is not our precise aim at Equilibrium, it is an important number to many investors that we can try to answer as mathematically as possible.
This is where the rule of 72 comes in.
So, what is it?
It is a simple way of calculating how long it could take for any investment to double in value. The calculation output is reliable but, of course, the investment return may vary.
How does it work?
In simple terms, if you divide 72 by the annual average expected return for an investment (compounded), your calculator will show you a rough estimate of how long (in years) it would take you to double your money.
Or in other words, 72 / expected investment return = years to double.
Obviously, there is some clever maths behind it, with the rule of 72 effectively being a simplified version of a “logarithmic calculation that involves complex functions like taking the natural log of numbers.” However, on the surface, the simple division of the two numbers will give a broad-brush answer to the investor.
For those that really wish to know, the precise formula looks like this:
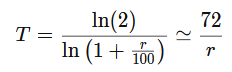
where:
T=Time to double
ln=Natural log function
r=Compounded interest rate per period
≃=Approximately equal to
Source: Investopedia
But for the purpose of this blog, let’s not get bogged down in the maths.
The table below simply shows how the rule of 72 works with the four traditional asset classes that are currently incorporated into our portfolios. These are based on long-term investment assumptions alongside the overall total assumed return for our Balanced Portfolio (net of our investment management fee):
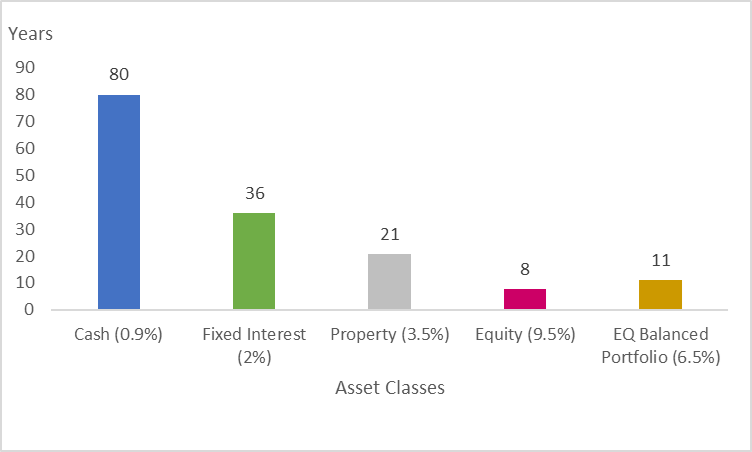
Source: Equilibrium Investment Management
As you can see, with an assumed growth rate of 0.9% from cash, it will take 80 years to double your money (before inflation) which is actually quite flattering if you consider current interest rates available on cash deposits (72/0.1 = 720 years!).
If you are holding excessive amounts of cash that is surplus to requirements, I would urge you to consider how these kinds of figures could impact your future financial position. However, a suitable emergency fund should always be retained.
If you take a relatively higher level of risk and invest in fixed interest, your return may increase to 2% and the time taken to double your money falls to 36 years.
Investing into property may provide a higher yield again, which could reduce the time taken to double your money to 21 years.
Clearly though, it is obvious that the quickest way to double your money is achieved by targeting higher returns by increasing exposure to equity. The issue with this, however, is that a higher level of volatility must be accepted to achieve it. This means that the risk to your capital is greater.
Returns from traditional asset classes, such as fixed interest (loans to governments and companies), and property (in this case, commercial property such as office blocks and retail parks, not the home you live in) could be much harder to come by over the next decade. Within our portfolios we are likely to increase exposure to other asset classes that do offer the potential for higher returns (in exchange for a higher level of volatility/risk) so that we can realistically look to achieve our target return over the long-term. It is important, however, that the right risk is taken in the right places. You might have seen this mentioned in the article,“Project Phoenix”, found in the latest edition of Equinox.
However, this doesn’t deter from the fact that a well-diversified asset mix is still key to managing risk, something we always look to do within our portfolios.
Looking at the figures for the Balanced Portfolio using the rule of 72, this suggests it would take 11 years to double your money (net of investment management fees). This could boast returns and reduce the time taken to double the money accordingly.
As we’ve seen, the rule of 72 can help us to quickly determine how long it could take to double a capital investment and it may seem a natural conclusion, therefore, that those looking to get 2x returns from their investments will need to accept a higher level of risk to get this to happen quicker.
However, we need to be wary of doing so, as higher risk can also lead to sharper and more exaggerated losses particularly in the short term. This will then lead to needing to recover to “point zero” before the rule of 72 could be reconsidered. We must also consider the accuracy of the expected investment return that is used in the calculation.
If you have any questions, or are interested to understand more about how we can help you, please don’t hesitate to get in touch by calling 0808 156 1176 or contacting us here.
The information provided in this blog is based on our opinion and is for general information purposes only. It should not be construed as financial advice. The information provided regarding taxes and allowances are based on our understanding of current rules and regulations, which may change. The impact of any tax changes will depend on individual circumstances.
